Multiwavelength Milky Way: Radiation Laws
The laws of light, energy, and temperature
![]()
I. The Stefan-Boltzmann law
II. Wien's law
III.Planck's law
Blackbody Radiation laws
I. The Stefan-Boltzmann law
II. Wien's law
blackbody - an object which absorbs all radiation falling upon it, and does not reflect any. All radiation emitted by a blackbody is due to its temperature. A star is a near perfect blackbody.
I. The amount of energy radiated by an object is related to its temperature. The
hotter the object, the more energy it releases. This idea is represented by the
Stefan-Boltzmann law
where Energy Flux (F) is the amount of energy emitted every second, σ (Greek symbol sigma) is the Stefan-Boltzmann constant (equal to 5.67 x 10-8 watts meter-2 K-4), and T is temperature in degrees kelvin (K). This law is best applied to a blackbody. The law says, for example, if you double an object's temperature, the amount of energy it releases increases by a factor of 16.
The Stefan-Boltzmann law is named after two Austrian physicists, Josef Stefan and Ludwig Boltzmann.
II. An object emits radiation at several wavelengths. However the peak wavelength
emitted depends on the object's temperature. The cooler the object, the longer the wavelength
at which most of the radiation is emitted. This is known as Wien's law
where λ (Greek symbol lambda) is wavelength, C is a constant, and T is temperature. If wavelength is measured in meters and temperature is measured in degrees kelvin, then C = 0.0029 (if wavelength is measured in nanometers, C = 29 x 105). This law is also best applied to a blackbody such as a star. The peak wavelength helps determine an object's color. If an object peaks in the ultraviolet portion of the electromagetic spectrum, more of its emitted radiation is on the violet/blue end of the visible spectrum than on the red end, so we see the object as being blue in color.
Wien's law is named after a German physicist, Wilhelm Wien.
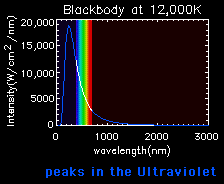
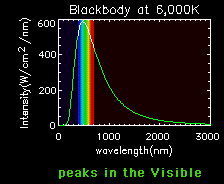
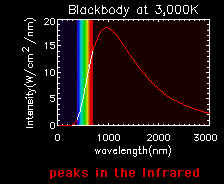
Blackbody curves are used to illustrate the Stefan-Boltzmann law and Wien's law. A hot object has a high curve (more total energy, Stefan-Boltzmann Law), which peaks at a short wavelength (Wien's Law). A cooler object has a low curve (less total energy), which peaks at a longer wavelength.
Back to top
Planck's Law
Light at a particular wavelength has a specific energy. This can be described as
where E is energy, h is Planck's constant, c is the speed of light, and λ (Greek symbol lambda) is wavelength. Planck's constant, h, is equal to 6.625 x 10-34 joules sec, which is the same as 4.135 x 10-15 eV sec (eV stands for "electron volt," and is a unit of energy like the joule is). This equation shows the relationship between the wave-like and particle-like nature of light, and is named after a German physicist, Max Planck. Planck's Law tells us that longer wavelengths have a lower energy than short wavelengths.
Back to top
Noteworthy:
In connection with COBE and the TARP (Technology And Research Partnership) project, two high school students have written a short discussion on
Blackbody radiation and Wien's Law.
Related Online Resources:
About Temperature - definition, history, and theory
Blackbody Radiation Graphs -
Plots and Quicktime movies for blackbody temperatures 500K-26,000K.
These links will take you outside of these pages. Use
your browser's back button or list of recently accessed pages to return.

