The QPipeline burst search algorithm

The QPipeline is an analysis pipeline for the detection of GWBs in data from interferometric gravitational wave detectors [10]. It is based on the Q-transform [12], a multi-resolution time-frequency transform that projects the data under test onto the space of Gaussian windowed complex exponentials characterized by a center time $\tau$, center frequency $\phi$, and quality factor $Q$.

$$X(\tau, \phi, Q) = \int_{-\infty}^{+\infty} x(t) \, e^{- 4 \pi^2 \phi^2 (t - \tau)^2 / Q^2} \, e^{-i 2 \pi \phi t} \, dt$$ (1)

The space of Gaussian enveloped complex exponentials is an overlapping basis of waveforms, whose duration $\sigma_t$ and bandwidth $\sigma_f$, defined as the standard deviation of the squared Gaussian envelope in time and frequency, have the minimum possible time-frequency uncertainty, $\sigma_t \sigma_f = 1 / 4 \pi$, where $Q = \phi / \sigma_f$.

There is good reason to select an overlapping basis of multi-resolution minimum-uncertainty functions. Absent detailed knowledge of the gravitational waveform, such a basis provides the tightest possible constraints on the time-frequency area of unmodeled signals, permitting the time-frequency distribution of signal energy to be non-coherently reconstructed while incorporating as little noise energy as possible. A choice of basis that does not have minimum time-frequency uncertainty would typically include more noise than necessary, decreasing signal to noise ratio. The exception would be a restricted search for a known set of waveforms, in which a matched filter search, where the template matches the target signal, would be optimal. This type of restricted search is not the focus of this paper. Another benefit of the tighter time-frequency constraints afforded by a multi-resolution sine-Gaussian template bank is the decreased likelihood for false coincidences, when testing for coincidence between multiple detectors.

In practice, the Q transform is evaluated only for a finite number of basis functions, also referred to here as templates or tiles. These templates are selected to cover a targeted region of signal space, and are spaced such that the fractional signal energy loss $-\delta Z/Z$ due to the mismatch $\delta \tau$, $\delta \phi$, and $\delta Q$ between an arbitrary basis function and the nearest measurement template,

$$\frac{-\delta Z}{Z} \simeq \frac{4 \pi^2 \phi^2}{Q^2} \, \de... ...Q^2} \, \delta Q^2 - \frac{1}{\phi Q} \delta \phi \, \delta Q,$$ (2)

is no larger than $\sim\!\!20\%$. This naturally leads to a tiling of the signal space that is logarithmic in Q, logarithmic in frequency, and linear in time.

The statistical significance of Q transform projections are given by their normalized energy $Z$, defined as the ratio of squared projection magnitude to the mean squared projection magnitude of other templates with the same central frequency and $Q$. For the case of ideal white noise, $Z$ is exponentially distributed, and related to the matched filter SNR $\rho$ [13] by the relation

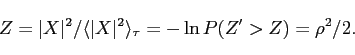$$Z = \vert X\vert^2 / \langle \vert X\vert^2 \rangle_{\tau} = - \ln P(Z^{\prime} > Z) = \rho^2 / 2.$$ (3)

The QPipeline consists of the following steps. The data is first whitened by zero-phase linear predictive filtering [14,10]. Next, the Q-transform is applied to the whitened data, and normalized energies are computed for each measurement template. Templates with statistically significant signal content are then identified by applying a threshold on the normalized energy. Finally, since a single event may potentially produce multiple overlapping triggers due to the overlap between measurement templates, only the most significant of overlapping templates are reported as triggers. As a result, the QPipeline is effectively a templated matched filter search [13] for signals that are Gaussian enveloped sinusoids in the whitened signal space.

Figure: The QPipeline view of the inspiral phase of a simulated optimally oriented 1.4/1.4 solar mass binary neutron star merger injected into typical single detector LIGO data with an SNR of 48.2 as measured by a matched filter search targeting inspiral signal. The QPipeline projects the whitened data onto the space of time, frequency, and $Q$. The left panel image shows the resulting time-frequency spectrogram of normalized signal energy for the value of Q that maximizes the measured normalized energy, while the right panel image shows the time-frequency distribution of only the most significant non-overlapping triggers regardless of $Q$.

Figure 1 shows an example of the QPipeline applied to the inspiral phase of a simulated binary neutron star coalescence signal injected into typical single detector LIGO data with an SNR of 48.2.