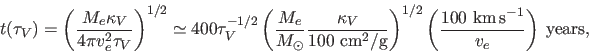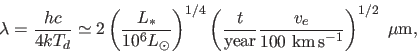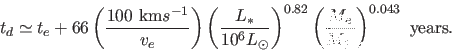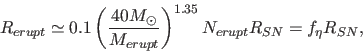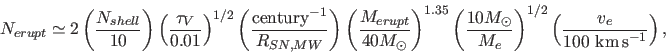Rate Limits
One advantage of searching for eruptions in the dust obscured phase is that the
process is relatively easy to simulate. We eject 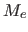 of material
from a star of luminosity
of material
from a star of luminosity 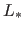 and temperature
and temperature 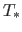 at velocity
at velocity 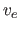 over
time period
over
time period 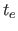 and assume it forms dust with total (absorption
plus scattering) visual opacity
and assume it forms dust with total (absorption
plus scattering) visual opacity 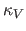 once it is sufficiently distant from the star. We
can then use DUSTY (Elitzur & Ivezic2001) to simulate the evolution of the mid-IR
luminosities and determine the time
once it is sufficiently distant from the star. We
can then use DUSTY (Elitzur & Ivezic2001) to simulate the evolution of the mid-IR
luminosities and determine the time 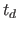 during which the source would
satisfy our selection criteria. Here we use
during which the source would
satisfy our selection criteria. Here we use 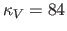 cm
cm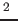 g
g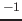 ,
roughly appropriate for silicate dust, but this is important only
to the extent that the ejecta mass can be rescaled as
,
roughly appropriate for silicate dust, but this is important only
to the extent that the ejecta mass can be rescaled as
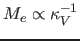 .
The key variable for estimating rates is the expansion velocity
.
The key variable for estimating rates is the expansion velocity 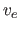 ,
because the detection period scales as
,
because the detection period scales as
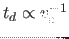 . The
velocities cited for the supernova impostors (e.g., Smith et al.2011)
and the velocity associated with the long axis of
. The
velocities cited for the supernova impostors (e.g., Smith et al.2011)
and the velocity associated with the long axis of 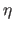 Car are
high,
Car are
high,
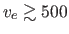 kms
kms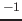 . These velocities are very different
from those observed for the older, massive shells in the Galaxy
or the shorter axis of
. These velocities are very different
from those observed for the older, massive shells in the Galaxy
or the shorter axis of 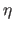 Car, where
Car, where
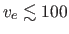 kms
kms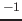 (see
the discussion of this difference in Kochanek2011a). Here
we scale the results to
(see
the discussion of this difference in Kochanek2011a). Here
we scale the results to 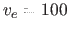 kms
kms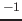 since, for example, it
results in our detecting systems with parameters similar to
since, for example, it
results in our detecting systems with parameters similar to 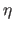 Car at its present age, as observed, and agrees with the expansion
velocities of the other massive Galactic shells around luminous stars.
Car at its present age, as observed, and agrees with the expansion
velocities of the other massive Galactic shells around luminous stars.
Detection of a shell at late times (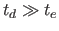 ) is limited by its
optical depth and temperature.
The shell has total visual optical depth greater than
) is limited by its
optical depth and temperature.
The shell has total visual optical depth greater than 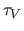 for
for
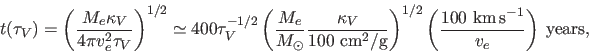 |
(4) |
and once 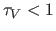 it begins to rapidly fade in the mid-IR. Ignoring
Planck factors, the spectral energy (
it begins to rapidly fade in the mid-IR. Ignoring
Planck factors, the spectral energy (
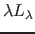 ) peaks at
) peaks at
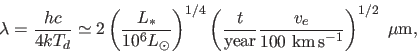 |
(5) |
so the emission peak shifts out of the IRAC bands after several decades,
and our survey is primarily limited by the shift of the emission
to longer wavelengths rather than the declining optical depth.
It is better to search for these sources at 24 as has been done in
the galaxy (Gvaramadze et al.2010; Wachter et al.2010) but that would
require the resolution of JWST (Gardner et al.2006).
A reasonable power-law fit to the results (
as has been done in
the galaxy (Gvaramadze et al.2010; Wachter et al.2010) but that would
require the resolution of JWST (Gardner et al.2006).
A reasonable power-law fit to the results (
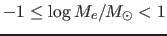 ,
,
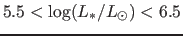 ) of the DUSTY models is that the detection period is
) of the DUSTY models is that the detection period is
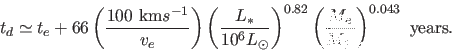 |
(6) |
For 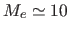 M
M and L
and L
 L
L like
like
 Car,
Car,
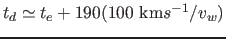 years
where
years
where 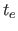 may also be
may also be 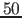 years or more (see the discussion
in Kochanek et al.2012a). For present purposes, we
adopt
years or more (see the discussion
in Kochanek et al.2012a). For present purposes, we
adopt 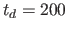 years as the period over which our selection
criteria would identify an analogue of
years as the period over which our selection
criteria would identify an analogue of 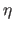 Car, consistent
with the fact that our selection criteria do identify
Car, consistent
with the fact that our selection criteria do identify 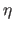 Car.
Car.
We can normalize the rate of eruptions to the ccSN rate as
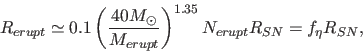 |
(7) |
where 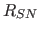 is the supernova rate and all stars more massive than
is the supernova rate and all stars more massive than 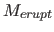 undergo
undergo 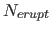 eruptions. Following the rate arguments in
Kochanek (2011a), we can estimate the number of eruptions
per massive star needed to explain the massive Galactic shells.
If there are
eruptions. Following the rate arguments in
Kochanek (2011a), we can estimate the number of eruptions
per massive star needed to explain the massive Galactic shells.
If there are
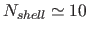 massive Galactic shells
associated with massive stars (
massive Galactic shells
associated with massive stars (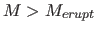 ), then
), then
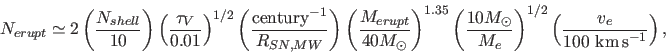 |
(8) |
where 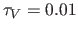 is the minimum optical depth needed to detect a shell
surrounding the star and
is the minimum optical depth needed to detect a shell
surrounding the star and
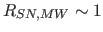 /century is the Galaxy's
supernova rate. Since the Galactic shells are identified as shells
primarily at
/century is the Galaxy's
supernova rate. Since the Galactic shells are identified as shells
primarily at 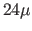 m, they are easier to find at low optical depths
and temperatures than in our extragalactic survey.
Thus, the massive Galactic shells imply an eruption
rate relative to the supernova rate of
m, they are easier to find at low optical depths
and temperatures than in our extragalactic survey.
Thus, the massive Galactic shells imply an eruption
rate relative to the supernova rate of
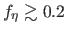 since it is unclear whether
we possess a complete inventory. Note that with this normalization
the rate estimate does not depend on the mass scale
since it is unclear whether
we possess a complete inventory. Note that with this normalization
the rate estimate does not depend on the mass scale 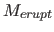 .
Rubab Khan
2012-10-28
.
Rubab Khan
2012-10-28
![]() ) is limited by its
optical depth and temperature.
The shell has total visual optical depth greater than
) is limited by its
optical depth and temperature.
The shell has total visual optical depth greater than ![]() for
for