 |
 |
Superfluid Pumps
Keeping the optics cold requires moving lots of liquid helium
(over ten liters per minute).
There are two potential problems.
First, pumps generally requires moving parts,
and moving parts do not fare well at cryogenic temperatures.
Second, at the low pressures encountered at ARCADE's
35 km flight altitude,
liquid helium cools enough to form a so-called "superfluid"
with zero viscosity or flow resistance.
A superfluid would thus slide off pump vanes
actually without being pumped.
ARCADE solves these problems by using fountain-effect pumps,
exploiting the strange properties of liquid helium
to pump large volumes with no moving parts.
At temperatures below 2.1768 K,
liquid helium undergoes a phase transition,
with part of the liquid falling into a superfluid state.
Superfluid helium has many strange properties,
but for ARCADE the following are most important:
(1) At non-zero temperature,
helium is a mixture of the normal and superfluid states.
The fraction of the liquid in the superfluid state
depends on the temperature,
and only on the temperature.
Just below the transition temperature
the liquid is nearly all in the normal state,
while just above absolute zero the liquid is nearly all
in the superfluid state.
At the ARCADE bath temperature of 1.5 K,
the liquid is roughly 90% superfluid
and 10% normal fluid.
(2) Superfluid helium has zero viscosity
and can move in a frictionless fashion
even in very restricted pipes.
(3) Superfluid helium has zero entropy;
energetically it is at absolute zero.
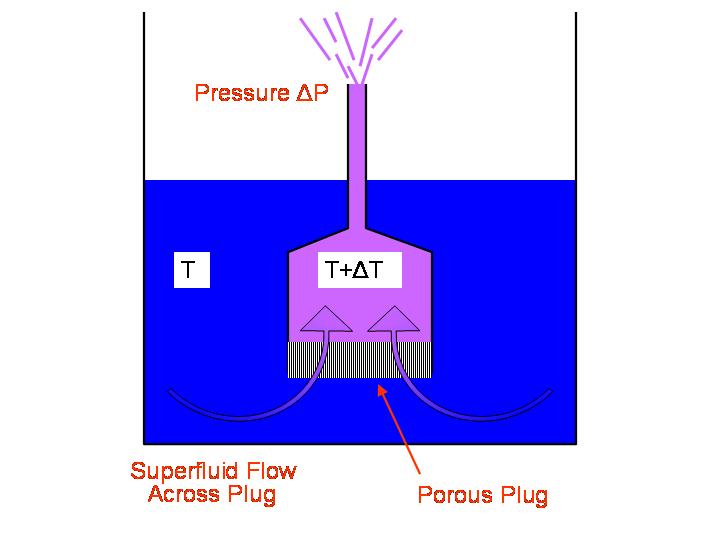
A fountain-effect pump consists of a tube
with a plug on one end and a heater inside.
The plug is porous,
with many very fine (sub-micron diameter) holes
that block the flow of normal liquid
while allowing free passage to the zero-viscosity superfluid.
Consider what happens if we turn on a heater inside the tube,
warming the liquid inside.
Warming the liquid converts some of the superfluid to normal fluid
(property 1 above).
Now there is a gradient across the plug,
with a higher percentage of superfluid on the outside than inside.
The superfluid thus flows through the plug
to reduce this gradient.
Since it has zero viscosity, the plug presents no impediment
(property 2 above).
But the fraction of the liquid in the superfluid state
can only depend on the temperature, which is fixed:
as the superfluid moves through the plug,
some if it gets converted to normal fluid.
The newly-minted normal fluid is blocked by the plug
and must remain in the tube,
and so the gradient remains
until the flow of liquid into the tube
increases the pressure enough
to counter the superfluid gradient across the plug.
A temperature difference as small as 0.1 K
will easily create enough pressure
to pump the liquid the entire 2 meter height of the ARCADE dewar.
We can use a little thermodynamics
to quantify the relation
between the applied temperature increase
and the resulting pressure head in the pump.
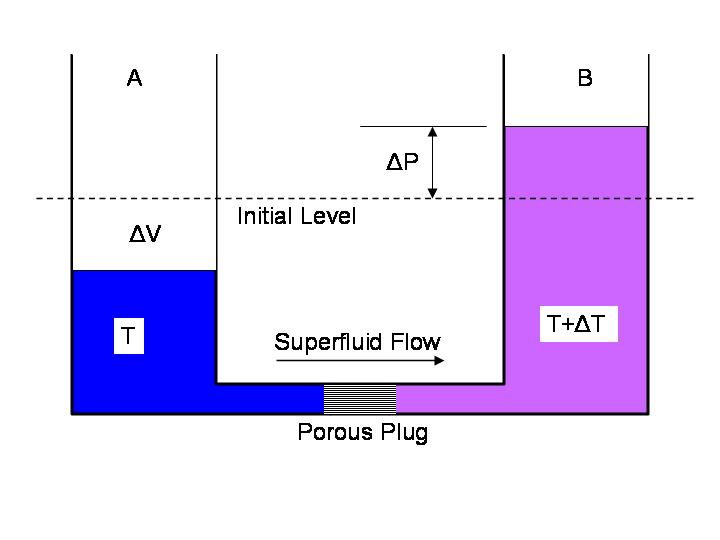
Consider two reservoirs of liquid helium
joined by a porous plug and initially at the same temperature T.
We add a fixed amount of heat Q_B to side B,
increasing its temperature by an amount dT.
As before, superfluid helium will flow across the plug from A to B.
The extra liquid stuck on side B
increases the volume on side B by an amount dV,
raising the liquid level
and creating a pressure head dP.
The gravitational work required to raise the liquid level is
W = dP * dV
Side A, meanwhile,
has lost some superfluid.
Losing superfluid would leave side A with
a higher fraction of normal fluid,
which by property (1) above
would imply a higher temperature on side A.
In order to keep the temperature on side A constant,
we must remove
an amount of heat Q_A from side A.
By conservation of energy, we then have
W = Q_B - Q_A
That is, the mechanical work against gravity
is given by the difference
between the heat supplied on side B
and the heat removed from side A.
The Second Law of Thermodynamics
allows us to specify the heat
Q_A or Q_B in terms of the entropy of the fluid:
Q_A = m S T
Q_B = m S (T + dT)
where m is the mass transferred from one side to the other
and
S is the specific entropy of the normal state liquid
(recall that the superfluid has zero entropy).
We can then combine the above equations to get
the pressure as a function of temperature increase:
dP = rho S dT
where
rho = m/V is the density of the liquid.
The pressure is proportional to the temperature difference
between the inside and the outside of the pump
(provided both remain below the superfluid transition at 2.1768 K).
Equivalently,
we can express the pressure head
in terms of the height of the helium column.
In practical units we obtain
h = 0.9 cm * (T/1.3 K)^5.6 * (dT/1 mK)
ARCADE uses over a dozen pumps to move tens of liters of helium per minute.
Since the huge ARCADE dewar has a large heat leak to the helium bath
regardless of what the instrument is doing,
we optimize the pump design for durability and ease of aseembly
rather than for minimum dissipated power.
The pumps are made from commercial plumbing fixtures.
The top left panel shows the bare pump body.
The top right panel shows the electrical inserts,
containing a pair of metal-film heater resistors
and a ruthenium oxide thermometer to monitor the pump temperature.
The bottom left panel shows the porous plug.
The ARCADE plugs are Coors-Tek P-1/2-BC porous ceramic,
cut to fit the plumbing fixture
and glued into place using
Stycast 2850-FT epoxy.
The bottom right panel shows the assembled pumps.
The electrical inserts are glued into the plumbing tee
opposite the porous plugs.
After assembly, we "paint" the body with a layer of Stycast
(not shown)
to minimize the parasitic heat flow from the pump interior
through the walls to the bath outside.
|
|