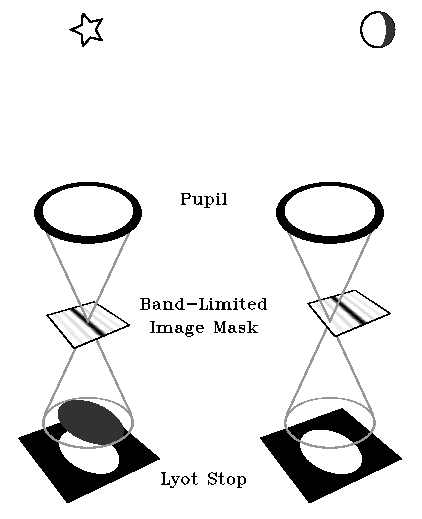
This figure illustrates schematically how a coronagraph works: light passes through the pupil and converges on an image mask, then the pupil is imaged onto a Lyot stop. Starlight focused on the center of the image mask diffracts to the pupil edges, where the Lyot stop can block it, as shown on the left of the figure. Light from an off-axis planet diffracts all around the second pupil plane, as shown on the right of the figure, and largely passes through the Lyot stop.
If you choose a ``band-limited'' image mask (Kuchner & Traub 2002) all of the light from an on-axis source diffracts to a region near of the edges of the pupil, so that a Lyot stop can block identically all of the light diffracted by the mask. Such an image mask typically consists of a series of dark rings or stripes. In the absence of other limiting factors, this design can completely block the light from an on-axis source, while providing up to 80\% throughput for off-axis planets, assuming a 10 m primary mirror at 0.5 microns, and an inner working distance of 30 milliarcseconds.
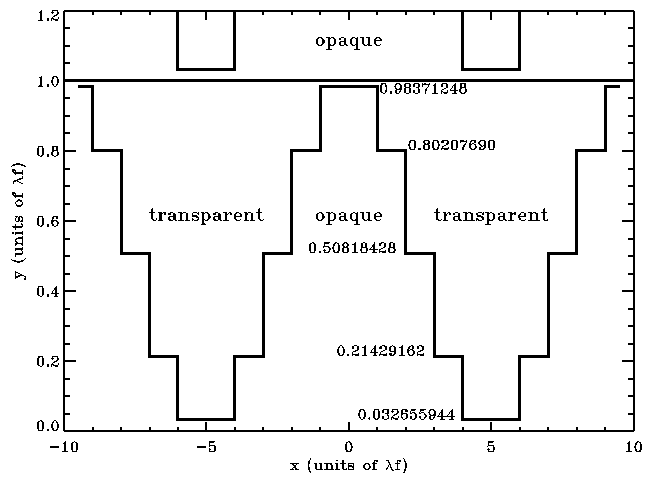
Image masks must be manufactured very precisely because they interact with focused light. A way around this problem is to use a ``notch filter'' mask (Kuchner & Spergel 2003). Here's a closeup of a sampled sine-squared notch filter mask with a bandwidth of 20%, meaning that the Lyot stop mut be smaller than the entrance pupil by 20%. The units are lamdba* f, the diffraction scale in the pupil plane. The heights of the opaque bars are
y=1.0081841792 - sin^2(0.1 pi (j+0.5)) , where j=...,-2,-1,0,1,2,....
All of the bars are lamdba* f wide. The top of one stripe does not quite touch the bottom of the next stripe.
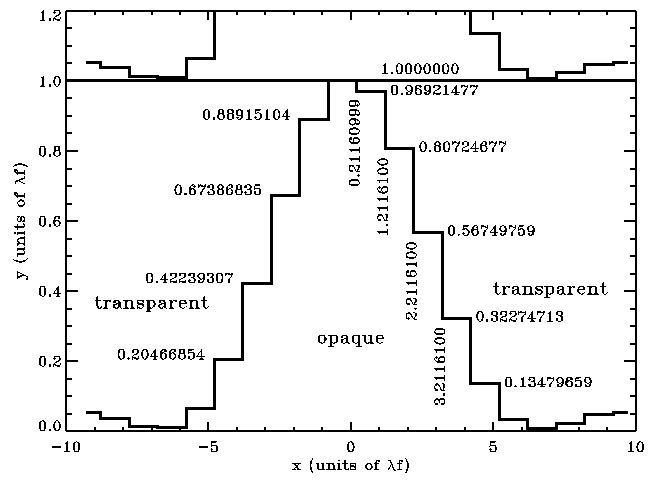
Here's a sampled 1-sinc-squared notch filter mask with a bandwidth of 30%. The heights of the opaque bars are
y=0.00614118 + sinc^2(0.15 pi (j-0.28839002)), where j=...,-2,-1,0,1,2,....
The top of one stripe touches the bottom of the next stripe. The bars are shifted to the left from being lined up with the coordinate grid. The longest bar covers the region from x=-0.78839001 to x=0.21160999.
Thanks to Doney Abraham and Daniel Hoppe for finding an error in this page!
References
Kuchner, M. J. & Traub W. A. 2002, ApJ, 570, 900, astro-ph/0203455
Kuchner, M. J. & Spergel, D. N. 2003, to appear in ApJ, astro-ph/0209271
Marc Kuchner's Home Page