How to read the JPL Ephemeris and Perform Barycentering
C. Markwardt
28 Jun 2001
This document describes how to read the JPL ephemeris table,
interpolate values, and perform barycentering. It also describes how
to make an intermediate table representation with Taylor series
coefficients for simpler operations.
JPL Ephemeris
The JPL Ephemeris tables, DE200 and DE405, describe the orbits of the
sun and planets with very high precision over relatively long time
scales. The DE200 ephemeris is "older" but more commonly used; the
DE405 is more recent and higher precision. Other differences are that
the DE200 ephemeris is nominally referenced to the FK5 coordinate
system, which is tied to nearby stars, whereas the the DE405 ephemeris
is referenced to the ICRS system, which is tied to distant radio
quasars.
One primary use for the ephemeris tables is for pulsar astronomy.
Knowledge of the planets' positions is required in order to convert
the time of arrival of a pulsar pulse into an inertial coordinate
system, namely the solar system barycenter (SSB). This procedure
involves both geometric corrections (the projected light travel time
to the SSB), but also relativistic corrections such as Shapiro time
delay and correction of clocks from the geocenter frame to the SSB
frame. For microsecond timing accuracy, all of these effects need to
be accounted for (e.g. Blandford & Teukolsky 1976; Taylor & Weisberg
1989).
Reading the JPL Ephemeris table is relatively straightforward but
requires some degree of bookkeeping. The file is stored as a series
of Chebyshev coefficients which can be interpolated to essentially any
desired temporal accuracy. It should be noted that there is only one
argument to the ephemeris, the time. In this case the time should be
expressed by clocks at the SSB (ie, in TDB).
Barycentering
To do proper pulsar timing, one must correct the earth-bound pulse
times of arrival to an inertial frame. The most convenient inertial
frame is that of the solar system barycenter. The correction process
can be expressed as follows:
tb = tobs + (clock) - (dispersion) + (geometric) + ("Einstein")
- ("Shapiro")
where
tobs - is the observed time of arrival
tb - is barycentric arrival time
(clock) - are the corrections which convert the local clock time to
geocentric TT or TDT.
(dispersion) - are dispersion corrections of the form D/fb^2
where fb is the barycentric frequency. D=0 for X-rays.
(geometric) - geometric time-delay in the solar system
("Einstein") - Einstein corrections - relativistic corrections of clock
time to SSB
("Shapiro") - Shapiro time delay due to photon bending in the potential
of the solar system
The "clock" corrections are observatory dependent. For XTE, after
applying the fine clock correction, times are directly expressed in
TT.
The "geometric" correction is the primary effect, which is essentially
the time for the photon to travel from earth to the SSB.
(geometric) = (robs . n)/c
where
robs - is the vector from the SSB to the observatory
n - is a unit vector pointing to the astrophysical source
The value of n depends on the position of the source on the sky (ie,
RA and DEC), is assumed to be known already, or is solved for in using
an iterative process.
For orbiting spacecraft, the vector robs can further be broken down
into components:
robs = rearth + rsat
where
rearth - is the vector from the SSB to the earth geocenter
rsat - is the vector from the earth geocenter to the spacecraft
rearth is completely specified by the JPL ephemeris. rsat is usually
determined from a separate satellite ephemeris table, such as an
"orbit" file. All of these vectors must be expressed in an inertial
coordinate frame.
The "Einstein" delay is the combined effect of gravitational redshift
and time dilation due to motions of the earth and other bodies, and is
caused by the time-varying gravitational potential and doppler shifts
experienced bythe observatory clock. To an accuracy of 1 ns, this
effect can be further broken down into two components:
("Einstein") = ("Einstein")_geo + (rsat . vearth)/c^2
where
("Einstein")_geo - is the effect as seen by a clock at the geocenter
vearth - is the velocity of the earth w.r.t. the SSB
The determination of the first quantity can now be realized
numerically using approximations such as Fairhead & Bretagnon 1990
or Fukushima 1995. The second term can be found using the earth and
satellite ephemerides. Combined, such codes are commonly known as
converting TT to TDB.
The "Shapiro" delay is the time delay analog of the well-known bending
of light near the sun. Its magnitude is
("Shapiro") = - (2 G Msun/c^3) log(1 + cos th)
where
th is the pulsar-sun-earth angle at the time of observation. Note that
this is *not* the pulsar-SSB-earth angle.
For a binary pulsar the computations are further complicated by the
fact that the pulsar itself is not in an inertial system. Therefore
there are additional corrections which must be applied.
For the purposes of barycentering, the primary uses of the JPL
Ephemeris table are in calculating rearth, vearth, and rsun (used in
calculating th).
Interpolating the JPL Ephemeris
The JPL ephemeris is a table of Chebyshev coefficients, that in and of
themselves do not give the planetary motions. These coefficients must
be entered into the simple Chebyshev polynomial equation with time as
a variable. The very first step is opening and reading the ephemeris
table, after which multiple interpolants can be constructed. Here I
will deal with the FITS file format of the JPL ephemeris table,
produced by Arnold Rots, and available in the AXBARY package for X-ray
astronomy, available from HEASARC (see below). The choice of which
table to use (DE200 or DE405) depends on the desired precision, the
coordinate system in use, and the desire to compare with previous
results.
I give some code examples, which are based on IDL syntax. The most
important difference between IDL and FORTRAN is that IDL arrays are
0-based, meaning that all array indices start with 0, while in FORTRAN
they start with 1. Thus, when transferring this code to FORTRAN, it
is important to add 1 to array indices. Unlike C, both IDL and
FORTRAN share the same convention about the ordering of
multidimensional array indices.
Opening and Reading the Ephemeris
The first step is to open and read the ephemeris table. Here I will
assume that the basic techniques of accessing FITS files is
well-known, so that I don't have to review the process.
The coefficients have a time dependence, which is first broken into
32-day intervals, and then further into a variable number of
sub-intervals, depending on the object. This ensures the maximum
temporal precision for the most quickly varying objects, but also
allows more slowly varying objects to have fewer terms. The
coefficients are actually stored in extension number 3 of the FITS
file, in a block format. The bookkeeping information in extension
number 2 allows a user to access the correct block of coefficients.
The FITS format file has three extensions beyond the primary
extension:
1. First ext. Contains various constants including
CLIGHT - speed of light (km/s)
EMRAT - earth-moon mass ratio (unitless)
AU - 1 A.U. (km)
GMS - Value of G * M_sun
RADS - solar radius (km)
These coefficients must be used downstream to ensure the correct
positions, etc. The units of GMS are such that GMS *
(AU/CLIGHT)^3 / 86400^2 is the value of G M_sun in units of light
seconds (ie, the gravitational radius in light seconds).
2. Second ext. Contains bookkeeping information for each planet
Object - Name of object (string)
Pointer - Starting index of coefficients (1-based)
NumCoeff - Number of coefficients per sub-interval
NumSubIntv - Number of subintervals per interval
Since each interval contains NSubIntv sub-intervals, each
sub-interval keeps NumCoeff coefficients, and there are 3 spatial
dimensions, there are a total of 3*NumCoeff*NumSubIntv
coefficients for each 32-day interval and each solar system
object.
3. The third ext. contains the raw coefficients. Each row contains
all of the coefficients for all of the bodies for a given 32-day
interval.
In my IDL program I open, read, and close the ephemeris table only
once during a single barycentering run. Before opening the ephemeris
file, I determine the extent of the times in the input file(s). That
way it is easy to know how many rows should be read from the
ephemeris. Generally speaking only a single ephemeris row (ie, a
single 32-day interval) is of interest, but there is always the
possibility that an observation spans two 32-day intervals, etc. For
safety's sake I always read the adjacent rows as well.
A summary of the operations I perform on opening and reading the
ephemeris table are as follows.
1. Open first extension and read constants listed above. I convert
all units to light-seconds where appropriate.
2. Open second extension and read all bookkeeping data. This is all
integer data, of a fixed size, so it is easy to pre-allocate the
correct arrays.
3. Open third extension and read coefficients for the desired rows.
Here I have an array with a dynamical number of rows, but a fixed
number of columns (ie, total number of coefficients for all
bodies in a 32-day interval).
In the subsequent interpolation calls, I also pass this data.
Interpolating the Ephemeris
The next stage is the actual interpolation of the ephemeris.
Normally, this is the most computationally expensive part of the
process, because it involves computing the positions of several solar
system bodies for many input times. The positions of the bodies must
be computed separately for each input file time. There are three
essential steps in performing this process: 1. compute SSB time
(Einstein delay); 2. determine which interval, and then which
sub-interval the time of interest falls in; 3. Compute Chebyshev
polynomial.
1. The computation of the SSB time is rather straightforward.
Performing this step is required because the argument of the ephemeris
itself is TDB time (ie, a clock referenced to the SSB). The two times
are different because of the gravitational potential difference and
doppler shifts between the earth and the SSB. In previous HEASARC
ephemeris tables (de200_new.fits), this value was tabulated supplied
as a separate column. It may be computed more conveniently perhaps by
using an analytical approximation (Fairhead & Bretagnon 1990).
Such a routine can be found in ctatv.c of the AXBARY package. However
it should be noted that this is a somewhat expensive function to
calculate, but it is also slowly varying, so in principle one should
be able to calculate the value only infrequently (once per 1-orbit
observation, say), without much penalty. Making the quantity
continuous is simple enough, by also estimating the derivative and
applying a first order drift correction (which is very small indeed).
After converting the time to the SSB, the time is known as "Ephemeris
Time".
2. As I already noted, the ephemeris is broken into 32-day intervals,
and from there, into a variable number of subintervals, depending on
the body. Also, coefficients for many bodies are stored in the table.
Thus, part of the challenge is to determine which subinterval to use.
First, to locate the correct range of coefficients for the body of
interest, one should determine Pointer, NumCoeff and NumSubIntv.
Then, the range of array values are from Pointer to
Pointer+NumCoeff*NumSubIntv*3, where Pointer is 1-based (ie FORTRAN).
The interval number, which is the row number in the table, is found by
simple rounding processes:
TINT = (T-JD0)/DT
IEPH = FLOOR(TINT)
where JD0 is the start date of the table, ie, the start time of the
first row; DT is 32 days; and T is the ephemeris time, expressed in
the same units as JD0 and DT, usually Julian days. The resulting
number, IEPH, is the 0-based row number in the table (ie, add 1 for
FORTRAN).
Next, the subinterval is chosen. The value of TINT is re-used here,
since it contains the residual time since the start of the interval.
TINT = (TINT-IEPH)*NumSubIntv ;; Note IEPH is 0-based here
NSEG = FLOOR(TINT)
The value of NSEG is the 0-based subinterval number. Finally, the
scaled Chebyshev time must be computed, which is to convert times over
the subinterval to the range [-1,+1]. This is done as following:
TSEG = 2*(TINT - NSEG) - 1
At this stage it should be relatively straightforward to see which
part of the coefficients array need to be accessed, since we know
precisely which body, row and subinterval are required. The
coefficients to be used are:
P = POINTER+NSEG*NumCoeff*3-1 ;; Start offset of subinterval
C(*) = ARRAY(IEPH, P:P+NumCoeff*3-1) ;; Extract coefficients
row offset
Here the IDL terminology are used, where arrays are 0-based. If the
FORTRAN notation is used, then a value of 1 should be added to IEPH
and P before accessing the coefficients array.
Thankfully the interval number and subinterval number do not change
frequently over the timescale of a typical X-ray observation. Thus,
it is possible to optimize the above calculations, to only be done
once, except when needing to cross a subinterval boundary. The
coefficients for the subinterval are stored as three separate arrays,
one each for X, Y and Z dimensions.
3. The final stage is to use the Chebyshev coefficients to interpolate
the function. Chebyshev polynomials are easy to compute, especially
because of a simple recurrence calculation. The first two polynomials
are defined explicitly:
T[0](x) = 1
T[1](x) = x
Subsequent polynomial terms can be found by using the recurrence
relation:
T[i](x) = 2*x*T[i-1](x) - T[i-2](x)
Here x is the scaled time TSEG found in the above computations. The
following IDL-style code gives an example of how to compute the values
for one of the dimensions.
IOFF = D*NumCoeff ;; Add 1 for FORTRAN (see below)
p0 = 1d ;; Establish first polynomials
p1 = TSEG
TT = 2D*TSEG ;; pre-compute scaled time (2*x) only once
R = C(IOFF) ;; first coefficient is explicit
for i = 1, NumCoeff-1 do begin
R = R + C(IOFF+I)*p1 ;; add next term
p2 = TT*p1 - p0 ;; compute next polynomial using recurrence
p0 = p1 ;; shift polynomials by one
p1 = p2
endfor
There are a few things to note. First, D is the dimension number,
which ranges from 0 for X to 2 for Z. The final result is the
position R, expressed in kilometers. Also, it should be recognized
that IDL is a 0-based language. For FORTRAN a value of 1 should be
added to IOFF in the first line. The same procedure should be applied
for X, Y and Z separately.
Also, users should be aware that there are differing conventions
regarding the specification of the zeroth Chebyshev coefficient.
Formally, the reconstructed function should take the form of
SUM(C(I)*T[I](X)) - 0.5*C(0), however this is form is clearly
redundant. The JPL tables specify C(0) such that the reconstructed
function is SUM(C(I)*T[I](X)), ie, the 0th coefficient has already
been divided by half.
To compute velocities, a similar approach is taken. The velocity of
the Chebyshev polynomials is readily computed by explicit derivatives.
In fact, it is simpler and more efficient to merge the position and
velocity computations into a single set of code, because the velocity
computation depends on the position polynomials. Here is a revised
set of code:
IOFF = D*NumCoeff ;; Add 1 for FORTRAN (see above)
p0 = 1d ;; Establish first polynomials
p1 = TSEG
v0 = 0 ;; First derivatives
v1 = 1
TT = 2D*TSEG ;; pre-compute scaled time once
R = C(IOFF+0) ;; first coefficient is explicit
VR = 0
for i = 1, NumCoeff-1 do begin
R = R + C(IOFF+I)*p1 ;; add next position term
VR = VR + C(IOFF+I)*v1 ;; add next velocity term
p2 = TT*p1 - p0 ;; compute next polynomial using recurrence
v2 = TT*v1 - v0 + 2*p1 ;; compute next velocity term using recurrence
p0 = p1 ;; shift polynomials by one
p1 = p2
v0 = v1
v1 = v2
endfor
Finally, the velocity must be scaled according to the number of
sub-intervals:
VR = VR * (2*NumSubIntv)/DT
which should result in a velocity in km/s. Typically one should be
able to derive predicted positions of solar system bodies to within a
few centimeters or better. In fact, this is probably more precise
than the actual planetary positions are known, however it maintains
the full accuracy of the JPL numerical integrations.
Handling Earth (special case)
You probably thought you were done by now, but you're not! There is
at least one more step when it comes to computing the position of the
earth, and that is because the JPL ephemeris does not contain the
position of the earth! Instead the table provides the position of the
earth-moon barycenter referred to the SSB, and the position of the
moon referred to the geocenter.
Thus, you must interpolate *both* the earth-barycenter and moon
ephemerides, and then combine them. In case you were wondering why
you needed the value of EMRAT, the earth-moon mass ratio, here is why.
Once you have interpolated both positions, then the position and
velocity of the earth geocenter, referred to the SSB, is found by the
following code:
EMRAT1 = 1D / (1D + EMRAT)
R_earth = R_earthmoon - EMRAT1 * R_moon
VR_earth = VR_earthmoon - EMRAT1 * VR_moon
Again, this must be done for each vector component, X, Y and Z.
Example
As an example, consider the position of the earth on
September 4, 1970. I use a Julian day 2440833.88056
(TDB) for the purposes of the example. The positions and
velocities of the earth on using the DE200
ephemeris are:
X 143881006.97775 km VX 8.79083 km/s
Y -42729783.17401 km VY 25.88305 km/s
Z -18536209.27272 km VZ 11.22465 km/s
[ Note: Ephemerides are also available by web, using the JPL HORIZONS
web page (see References). You should be aware that these ephemerides
are based on the JPL DE406, which covers a much longer time baseline
than DE200, with lower accuracy. Thus, you should not try to compare
the DE406 and DE200/405 numbers directly. ]
Constructing Daily Taylor Series
If the prospect of doing all of the above appears to be rather
daunting, then you may wish to perform the bulk of the computation
once, and then save some intermediate results. In fact, this is the
approach that (unknown authors) took in constructing de200_new.fits.
Here they provided a much simplified format. This file has been
supplied by HEASARC with the FTOOLS package for many years.
Unfortunately the coverage of the file expired at the end of the year
2000, so I have undertaken to generate a new file.
The file has three main columns:
1. Daily Earth position Taylor coefficients (4 coeff x 3 components)
2. Daily Sun position (absolute position)
3. Daily TTtoTDB offset value
The benefits of this file over the full JPL Ephemeris, at least for
the purposes of X-ray astronomy, is that the positions of only a few
bodies are stored, they are stored on a uniform rather than
non-uniform time grid, and that the Taylor series is straightforward
to develop. Finally, the storage of the TTtoTDB "time ephemeris"
avoids the need to calculate it analytically.
The file has one row for each day, centered on Julian noon. Thus, a
single row might cover from Julian day number 2451910.5 to 2451911.5,
in other words the entire day of 01 Jan 2001, from 00:00 to 24:00.
Thus, accessing this table is slightly easier than the full Chebyshev
method, because you simply divide the Julian time of interest into
integer and fractional parts. The division should be such that the
fractional part runs from -0.5 to +0.5. For example, a Julian date of
2440833.88056 would be divided into an integer part 2440834 and
fractional part -0.11944. This operation can be effected simply by a
rounding operation:
TC = ROUND(T) ;; Integer part
TF = T-TC ;; Fractional part
The earth position is formed using a Taylor series:
X = C(0) + C(3)*TF + C(6)*TF^2 / 2 + C(9 )*TF^3 / 6
Y = C(1) + C(4)*TF + C(7)*TF^2 / 2 + C(10)*TF^3 / 6
Z = C(2) + C(5)*TF + C(8)*TF^2 / 2 + C(11)*TF^3 / 6
Where C is the array of coefficients for a particular day, and TF is
the fractional part of the day, computed above. [ Note that 0-based
IDL-style indexing is used here. ]
How does one go about regenerating such a file? My approach is
perhaps a bit circuitous, but I believe it to be optimal. I
recognized that the Chebyshev polynomials are a natural form of
approximation, and it is actually quite easy to compute the
coefficients for a low-order approximation. The Chebyshev
approximation is also usually quite "optimal" in the sense that the
error rapidly decreases with number of terms, and is never more than
the next coefficient. For a cubic approximation, the first four
Chebyshev coefficients must be computed. Once they are computed,
there is a natural and exact conversion to Taylor series coefficients.
Thus, the chain of approximation takes the following approach:
1. Determine body position at fixed times during day from JPL
ephemeris
2. Construct Chebyshev approximation from those points
3. Convert new Chebyshev coefficients into Taylor series coefficients
You may ask why the original JPL coefficients cannot be used directly.
However, one must remember that the JPL ephemeris is sampled with a
variable number of sub-intervals (not daily), and has a variable
number of coefficients. Also, for the earth, there is the
complication that the positions of *two* bodies must be computed
(earth-moon barycenter and moon alone). Thus, it would be very
difficult to simply convert the JPL coefficients to another form.
Instead, I assume that the ephemeris is a general function f(X) which
can be evaluated at arbitrary abscissae with arbitrary precision. The
I apply some tests below to see how precise the approximation is.
Assume that the position of the earth on a given single day is
represented by the function f(X) where X ranges from [-1,+1]. In
other words, X = 2*TF-1, where TF is the fractional day.
The Chebyshev coefficients can be found by direct algebraic
manipulation of the Chebyshev polynomials, however, by exploiting the
orthogonality conditions, an explicit expression for the coefficients
can be found in terms of the function evaluated at four points in the
interval. These points are Xnode = [ C18, C38, -C38, -C18], where C18
is cos(!dpi/8) and C38 is cos(3*!dpi/8). The values of the function
at these points shall be referred to as F1, F2, F3 and F4,
respectively. The explicit expressions for the Chebyshev coefficients
are then:
C0 = (F1+F2+F3+F4)/4
C1 = ((F1-F4)*C18 + (F2-F3)*C38)/2
C2 = (F1-F2-F3+F4)/sqrt(8)
C3 = ((F1-F4)*C38 + (F3-F2)*C18)/2
From there, it is also relatively straightforward to form the Taylor
series expansion
F(X) = A0 + A1*X + A2*X^2/2 + A3*X^3/6
and by equating it to the Chebyshev expression, one can derive similar
explicit expressions for A0 to A3:
A0 = C0 - C2
A1 = C1 - 3*C3
A2 = 4*C2
A3 = 24*C3
Finally, when converting this to back to the system where time is
again measured in days (ie, (t-day) ranges from -0.5 to +0.5), then
one arrives at the following modified coefficients:
A0' = A0
A1' = A1 * 2
A2' = A2 * 4
A3' = A3 * 8
This set of coefficients must be computed separately for each vector
component of the earth's position, and stored in a single row of the
"Earth" column of the output FITS file. The format of a single cell
is [X0, Y0, Z0, X1, Y1, Z1, X2, Y2, Z2, X3, Y3, Z3], where the Di
is the ith Taylor coefficient for the Dth dimension.
The velocity of the earth can be computed from these coefficients by
taking a derivative of the Taylor series approximation (ie, A1 + A2*X
+ A3*X^2/2). The position of the sun is supplied only at noon on each
day (ie, not even a first order approximation). Finally, the TDBtoTT
computation is performed based on the Fairhead & Bretagnon et al
algorithm, with one value per day.
The new ephemeris is computed from noon 10 Dec 1959 to noon 2049 Dec
31 (Julian days from 2436913 to 2469807). I chose that particular
start date to match the existing de200_new.fits file, so that software
with hardwired dates will not crash. The resulting file was based on
the JPL DE200 ephemeris. There is no barrier to computing an
additional table based on the DE405 ephemeris.
Testing Taylor Series Error
There is a significant overlap between the de200_new.fits file and my
new ephemeris based on DE200. In that overlapping region there is a
slight difference between the two files. The resulting positions
differ by 200-300 nano-light-seconds. In principle this will not be a
problem for XTE, whose clock is limited to ~5 usec accuracy. However
the slight differences made me curious. Why are they not exactly the
same?
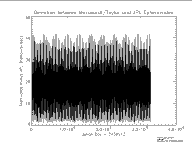 |
Plot of absolute deviation between Markwardt (Taylor series) and
full JPL Chebyshev ephemeris, expressed in nano light seconds. |
I did two checks. In the first check I compared my new table against
the original DE200 ephemeris. I did this on a grid of 30 points each
day, recording the maximum Euclidean distance between the original
Chebyshev-derived JPL ephemeris, and my new Taylor-approximated
ephemeris. I found that the maximum error, is on the order of 45
nano-light-seconds over the entire 90 year time span. The time
profile of this deviation oscillates in a non-obvious way, with
periods on a number of timescales. I believe these deviations are due
to short timescale variations in the earth position during one day,
proably due to effects like lunar tidal forces. In any case,
deviations of < 45 nano- lt-seconds are quite good.
I also examined the deviations on a small scale. I chose two
particular days to examine, one of them had the maximum error, and the
other the minimum error. Obviously, any other days would be
intermediate. I interpolated the JPL, Markwardt, and old FTOOLS
ephemerides with 1000 points per day. I also allowed 10% overlap with
the preceding and following days, so the total number of points was
1200. Finally, I plotted the Euclidean deviation between the JPL
ephemeris and the other two. The (Markwardt-JPL) deviation is plotted
with dashed lines, while the (FTOOLS-JPL) deviation is plotted with
solid lines.
The minimum error day was centered on Julian day 2440286, and the
maximum error day was on 2440210. Here I only considered those dates
before the year 2001, so that it would be possible to use the old
FTOOLS table.
 |
Julian day 2440286. Plot of deviations between full JPL
ephemeris, and Markwardt series (dashed) and old FTOOLS series
(solid). This day represents the day with smallest deviations. |
The low error day was clearly just that: the deviation between the
Markwardt and JPL ephemerides was within a few nano lt-seconds.
Nothing much else is remarkable about that particular day. However,
it is important to see that the deviations from the surrounding days
is significant. To me, this says that the error is simply
fortuitously small on day 2440286, and there is no reason to suspect
that the error could be reduced to the same level for all days.
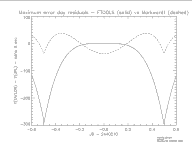 |
Julian day 2440210. Plot of deviations between full JPL
ephemeris, and Markwardt series (dashed) and old FTOOLS series
(solid). This day represents the day with largest
deviations. |
In the maximum error day plot we can see much larger deviations. The
Markwardt table is within 50 nano lt-seconds of the JPL ephemeris,
while the old FTOOLS ephemeris is within 300 nano lt-seconds. It
should be clear that both of these tables are suitable for X-ray
timing for the foreseeable future, even at their worst. Currently, the
best timing available is from RXTE, which has a formal 5000 nano
second fine clock jitter.
It is worth pointing out the differences between the two
approximations. The Markwardt table is based on optimally sampling
the function at four points throughout the day, and results in a
function which has error smoothly distributed throughout the day as
well. [For example, the deviation at noon is non-zero. ] This is a
natural, and desirable, property of the Chebyshev approximation. The
residual pattern is typical, appearing as a fourth order polynomial
(ie, the next unmodelled order).
The old FTOOLS approximation appears to be quite good near noon time,
in fact much better than the Chebyshev approximation within +/- 0.2
days of noon, but the deviation grows progressively worse as time
tends to midnight in either direction. This suggests to me that the
authors chose to interpolate the JPL ephemeris using an iterative
approach (for example, evaluate function at noon; subtract constant;
fit linear model; subtract line; fit quadratic model; etc.). Such a
technique is adequate but not optimal.
Finally, I also examined the difference between the TT to TDB
conversion in the old FTOOLS and the Markwardt table. I found that
they agree to +/- 30 nano seconds.
As I already mentioned, both tables are of sufficient quality to meet
the needs of most missions for the foreseeable future. Still, the
interpolation improvement is not hard to implement, so it doesn't hurt
to include it. The primary reason to adopt the newer Taylor ephemeris
is the greater time coverage. For maximum precision interpolation,
however, one should use the original JPL ephemeris, which has the
advantages that they are officially sanctioned; also, the function
appears to be more continuous at interval boundaries than the Taylor
approximation.
References
Blandford, R. & Teukolsky, S. A. 1976, ApJ, 205, 580
Fairhead, L. & Bretagnon, P. 1990, A&A, 229, 240
Fukushima, T. 1995, A&A, 294, 895
Press, Teukolsky, Vettering, Flannery, *Numerical Recipes in C*, 2nd Ed.
Taylor J. H. & Weisberg, J. M. 1989, ApJ, 345, 434
AXBARY Package
ftp://heasarc.gsfc.nasa.gov/xte/calib_data/clock/bary/
HORIZONS Web Page
http://ssd.jpl.nasa.gov/horizons.html
EPHEMERIDES DISCUSSED
JPLEPH.200 - JPL DE200 Ephemeris, full Chebyshev
de200_new.fits - "Old" FTOOLS ephemeris, daily Taylor series
de200_1950-2050_v2.fits - New Markwardt ephemeris, daily Taylor series,
good to < 45 ns
de200_1950-2050.fits - Markwardt ephemeris, good to < 85 ns
Return to Craig Markwardt's Homepage



