University of Washington Big G Measurement

Jens H. Gundlach and Stephen M. Merkowitz

Since Cavendish first measured Newton's Gravitational constant 200 years ago, "Big G" remains one of the most elusive constants in physics. The value of big G tells us how much gravitational force acts between two masses separated by a known distance. In Einstein's language of general relativity, it tells us the amount of space-time curvature due to a given mass. Together with Planck's constant and the speed of light it is considered to be one of the most fundamental constants in nature. Big G is a necessary ingredient in determining the mass of the earth, the moon, the sun and the other planets.

Several measurements in the past decade did not succeed in improving our knowledge of big G's value. To the contrary, the variation between different measurements forced the CODATA committee, which determines the internationally accepted standard values, to increase the uncertainty from 0.013% for the value quoted in 1987 to the twelve times larger uncertainty of 0.15% for the 1998 "official" value. This situation is an embarrassment to modern physics, considering that the intrinsic strength of electromagnetism, for instance, is known 2.5 million times more precisely and is steadily being improved. (The situation of G becomes more understandable if one considers the weakness of gravity: the total gravitational force twisting on the pendulum of a typical Cavendish torsion balance is only equivalent to the weight of a bacteria and that small force must be measured very precisely.)

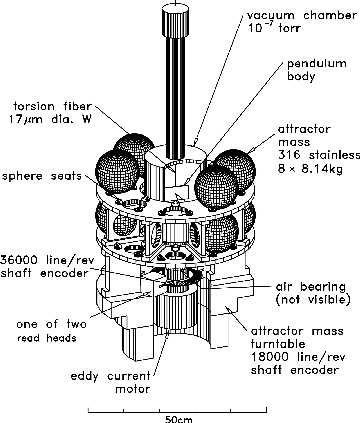
We built a highly modified and untraditional version of the 200-year-old Cavendish torsion balance apparatus and conducted a measurement of G that surpasses the precision of any previous measurement by far. We implemented several novel and elegant tricks to avoid the known systematic problems. These tricks make our measurement much more reliable.

Our torsion balance is installed on a turntable that rotates with about one revolution per 20 minutes between a set of source (attractor) masses. As the balance rotates, the gravitational forces exerted by the source masses try to twist the torsion fiber. However, our computer-controlled system adjusts the speed of the turntable exactly so that it always catches up with the pendulum. We record the acceleration of the turntable with a precision angle-measuring device and a stable clock. We then calculate G directly from these acceleration data. The Japanese physicist Kazuaki Kuroda was the first to point out that traditional Cavendish experiments that need to twist the torsion fiber will give too high a value for G; in our experiment there is no twist.

Instead of the traditionally-used dumbbell shape for the pendulum, we discovered that it is far better to use a thin flat rectangular plate hung vertically. With this shape we do not need to know the precise dimensions, mass, or mass distribution of the pendulum itself. In previous measurements the experimenters had to precisely survey their pendulum and this led to their largest quoted uncertainty in G.

Flat plate pendulum.

The source masses used in our instruments are a number of precisely machined stainless steel spheres (cantaloupe-sized ball bearings). We use four or eight of the spheres at a time, positioning them on a turntable that rotates around the pendulum turntable, but in the opposite direction and at a much faster speed. This makes our signal easily distinguishable from gravitational forces between other objects in the laboratory. The signal of interest is also at a higher frequency where it is much easier to extract and less noisy.

The analysis of our measurements gives us an uncertainty of only about 0.0014% and, therefore, our value for G presents a substantial improvement. Our value for G is

Combining this value for with the orbits of the Lageos satellites gives us a mass of Earth of

This work was supported by a grant from the National Institute of Standards and Technology and by funding from the National Science Foundation, as well as with tremendous help from the Physics Department and from the Nuclear Physics Laboratory at the University of Washington.

Videos

• Full view video of the rotating apparatus.
• Closeup view video of the rotating apparatus.

Further Reading

1. "Measurement of Newton's Constant Using a Torsion Balance with Angular Acceleration Feedback," Jens H. Gundlach and Stephen M. Merkowitz, Phys. Rev. Lett. 85, 2869 (2000).
2. "Our Knowledge of G Gets Worse, Then Better," Bertram Schwarzschild, Physics Today (July 2000)
3. "New technique for measuring Newton's constant G," J. H. Gundlach, E. G. Adelberger, B. R. Heckel, and H. E. Swanson, Phys. Rev. D 54, R1256 (1996).
4. The Controversy over Newton's Gravitational Constant